知识点:《相似三角形中考题》 收集:傅沂排 编辑:杜鹃花妹子
本知识点包括:1、今年初三了,明年就的中考了,可我数学那啥三角形对... 2、怎么解中考数学压轴题:一般是二次函数,三角形相似.... 3、如何解答中考圆与相似三角形的问题 4、中考数学证明题为什么不能用相似三角形做 5、有关2016年中考数学试题中相似三角形的题?一道大... 。
《相似三角形中考题》相关知识
《相似三角形》中考复习题及答案
一.选择题
(1)△ABC中,D、E、F分别是在AB、AC、BC上的点,DE∥BC,EF∥AB,那么下列各式正确的是( )
A.= B.= C.= D.=
(2)在△ABC中,BC=5,CA=45,AB=46,另一个与它相似的三角形的最短边是15,则最长边是( )
A.138 B. C.135 D.不确定
(3)在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,则构成的三个三角形中,相似的是( )
A.△ABD∽△BCD B.△ABC∽△BDC
C.△ABC∽△ABD D.不存在
(4)将三角形高分为四等分,过每个分点作底边的平行线,将三角形分四个部分,则四个部分面积之比是( )
A.1∶3∶5∶7 B.1∶2∶3∶4 C.1∶2∶4∶5 D.1∶2∶3∶5
(5)下列命题中,真命题是( )
A.有一个角为30°的两个等腰三角形相似 B.邻边之比都等于2的两个平行四边形相似
C.底角为40°的两个等腰梯形相似 D.有一个角为120°的两个等腰三角形相似
(6)直角梯形ABCD中,AD为上底,∠D=Rt∠,AC⊥AB,AD=4,BC=9,则AC等于( )
A.5 B.6 C.7 D.8
(7)已知CD为Rt△ABC斜边上的中线,E、F分别是AC、BC中点,则CD与EF关系是( )
A.EF>CD B.EF=CD C.EF<CD D.不能确定
(8)下列命题①相似三角形一定不是全等三角形 ②相似三角形对应中线的比等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O是△ABC内任意一点.OA、OB、OC的中点连成的三角形△A′B′C′∽△ABC.其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
(9)D为△ABC的AB边上一点,若△ACD∽△ABC,应满足条件有下列三种可能①∠ACD=∠B ②∠ADC=∠ACB ③AC2=AB·AD,其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
(10)下列命题错误的是( )
A.如果一个菱形的一个角等于另一个菱形的一个角,则它们相似
B.如果一个矩形的两邻边之比等于另一个矩形的两邻边之比,则它们相似
C.如果两个平行四边形相似,则它们对应高的比等于相似比
D.对应角相等,对应边成比例的两个多边形相似
二、填空题
(1)比例的基本性质是________________________________________
(2)若线段a=75px,b=300px,a、b的比例中项c=________,a、b、c的第四比例线段d=________
(3)如下图,EF∥BC,若AE∶EB=2∶1,EM=1,MF=2,则AM∶AN=________,BN∶NC=________
(4)有同一三角形地块的甲乙两地图,比例尺分别为1∶200和1∶500,则甲地图与乙地图的相似比为________,面积比为________
(5)若两个相似三角形的面积之比为1∶2,则它们对应边上的高之比为________
(6)已知CD是Rt△ABC斜边AB上的高,则CD2=________
(7)把一个三角形改成和它相似的三角形,如果边长扩大为原来的10倍,那么面积扩大为原来的____倍,周长扩大为原来的______倍.
(8)Rt△ABC中,∠C=90°,CD为斜边上的高.若AC∶AB=4∶9,则AD∶BD=________
(9)把1550px的线段分成三部分,它们的比为3∶2∶5,则最长段为________
(10)若D为△ABC边BC之中点,E为AD的中点,BE交AC于F,则AF∶FC=________
三、.已知平行四边形ABCD中,AE∶EB=1∶2,求△AEF与△CDF的周长比,如果S△AEF=150px2,求S△CDF.
四.如下图,已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E.求证:DE2=BE·CE.
五、已知如图,在平行四边形ABCD中,DE=BF,求证:=.
六、过△ABC的顶点C任作一直线,与边AB及中线AD分别交于点F和E,求证:AE∶ED=2AF∶FB.
七、如果四边形ABCD的对角线交于O,过O作直线OG∥AB交BC于E,交AD于F,交CD的延长线于G,求证:OG2=GE·GF.
八、如下图,在△ABC中,D、E分别为BC的三等分点,CM为AB上的中线,CM分别交AE、AD于F、G,则CF∶FG∶GM=5∶3∶2
九、如下图,△ABC中,AD∥BC,连结CD交AB于E,且AE∶EB=1∶3,过E作EF∥BC,交AC于F,S△ADE=50px2,求S△BCE,S△AEF.
十、已知:线段AB,分点C将AB分成3∶11两组,分点D将AB分成5∶9两段,且CD=100px,求AB的长.
十一、下图中,E为平行四边形ABCD的对角线AC上一点,AE∶EC=1∶3,BE的延长线交CD的延长线于G,交AD于F,求证:BF∶FG=1∶2.
参考答案
一..(1)C (2)A (3)B (4)A (5)D (6)B (7)B (8)C (9)D (10)D
二.(1)略 (2)6,24 (3)2∶3,1∶2 (4)5∶2;25∶4 (5)∶2 (6)AD·BD (7)100,10 (8)16∶65 (9)31 (10)1∶2
三.1∶3,S△CDF=1350px2
四.提示:连接AE,则AE=DE,证△AEC∽△BEA
五.略 六.略
七.提示:过E点作EH∥BD交CD于H,连接HO,由=得HO∥AD,这时=,由OD∥EH,得=,即可证
八、略
九.提示:连接MD,证F为MC中点,MD=2EF,AE=2MD,∴CF∶GF∶GM=5∶3∶2
十.S△BCE=450px2 S△AEF=37.5px2 282px
十一略.
十二.△AEF∽△CEB,AF∶BC=AF∶AD=1∶3,则AF∶FD=1∶2,又△ABF∽△GDF,则BF∶FG=1∶2
2012中考数学压轴题函数相似三角形问题(三)
例5
如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
(1)求此抛物线的解析式;
(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的 点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.
,
图1
动感体验
请打开几何画板文件名“09临沂26”,拖动点P在抛物线上运动,可以体验到,△PAM的形状在变化,分别双击按钮“P在B左侧”、“ P在x轴上方”和“P在A右侧”,可以显示△PAM与△OAC相似的三个情景.
双击按钮“第(3)题”, 拖动点D在x轴上方的抛物线上运动,观察△DCA的形状和面积随D变化的图象,可以体验到,E是AC的中点时,△DCA的面积最大.
思路点拨
1.已知抛物线与x轴的两个交点,用待定系数法求解析式时,设交点式比较简便.
2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长.
3.按照两条直角边对应成比例,分两种情况列方程.
4.把△DCA可以分割为共底的两个三角形,高的和等于OA.
满分解答
(1)因为抛物线与x轴交于A(4,0)、B(1,0)两点,设抛物线的解析式为,代入点C的 坐标(0,-2),解得.所以抛物线的解析式为.
(2)设点P的坐标为.
①如图2,当点P在x轴上方时,1<x<4,.
如果,那么.解得不合题意.
如果,那么.解得.
此时点P的坐标为(2,1).
②如图3,当点P在点A的右侧时,x>4,.
解方程,得.此时点P的坐标为.
解方程,得不合题意.
③如图4,当点P在点B的左侧时,x<1,.
解方程,得.此时点P的坐标为.
解方程,得.此时点P与点O重合,不合题意.
综上所述,符合条件的 点P的坐标为(2,1)或或.
图2 图3 图4
(3)如图5,过点D作x轴的垂线交AC于E.直线AC的解析式为.
设点D的横坐标为m,那么点D的坐标为,点E的坐标为.所以.
因此.
当时,△DCA的面积最大,此时点D的坐标为(2,1).
图5 图6
考点伸展
第(3)题也可以这样
如图6,过D点构造矩形OAMN,那么△DCA的面积等于直角梯形CAMN的面积减去△CDN和△ADM的面积.
设点D的横坐标为(m,n),那么
.
由于,所以.
例6
如图1,△ABC中,AB=5,AC=3,cosA=.D为射线BA上的点(点D不与点B重合),作DE//BC交射线CA于点E..
(1) 若CE=x,BD=y,求y与x的函数关系式,并写出函数的定义域;
(2) 当分别以线段BD,CE为直径的两圆相切时,求DE的长度;
(3) 当点D在AB边上时,BC边上是否存在点F,使△ABC与△DEF相似?若存在,请求出线段BF的长;若不存在,请说明理由.
图1 备用图 备用图
动感体验
请打开几何画板文件名“09闸北25”,拖动点D可以在射线BA上运动.双击按钮“第(2)题”,拖动点D可以体验到两圆可以外切一次,内切两次.
双击按钮“第(3)题”,再分别双击按钮“DE为腰”和“DE为底边”,可以体验到,△DEF为等腰三角形.
思路点拨
1.先解读背景图,△ABC是等腰三角形,那么第(3)题中符合条件的△DEF也是等腰三角形.
2.用含有x的式子表示BD、DE、MN是解答第(2)题的先决条件,注意点E的位置不同,DE、MN表示的形式分两种情况.
3.求两圆相切的问题时,先罗列三要素,再列方程,最后检验方程的解的位置是否符合题意.
4.第(3)题按照DE为腰和底边两种情况分类讨论,运用典型题目的结论可以帮助我们轻松解题.
满分解答
(1)如图2,作BH⊥AC,垂足为点H.在Rt△ABH中,AB=5,cosA=,所以AH==AC.所以BH垂直平分AC,△ABC 为等腰三角形,AB=CB=5.
因为DE//BC,所以,即.于是得到,().
(2)如图3,图4,因为DE//BC,所以,即,.因此,圆心距.
图2 图3 图4
在⊙M中,在⊙N中,.
①当两圆外切时,.解得或者.
如图5,符合题意的解为,此时.
②当两圆内切时,.
当x<6时,解得,如图6,此时E在CA的延长线上,;
当x>6时,解得,如图7,此时E在CA的延长线上,.
图5 图6 图7
(3)因为△ABC是等腰三角形,因此当△ABC与△DEF相似时,△DEF也是等腰三角形.
如图8,当D、E、F为△ABC的三边的中点时,DE为等腰三角形DEF的腰,符合题意,此时BF=2.5.根据对称性,当F在BC边上的高的垂足时,也符合题意,此时BF=4.1.
如图9,当DE为等腰三角形DEF的底边时,四边形DECF是平行四边形,此时.
图8 图9 图10 图11
考点伸展
第(3)题的情景是一道典型题,如图10,如图11,AH是△ABC的高,D、E、F为△ABC的三边的中点,那么四边形DEHF是等腰梯形.
例 7
如图1,在直角坐标系xOy中,设点A(0,t),点Q(t,b).平移二次函数的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B、C两点(∣OB∣
知识拓展:
1:二次函数图像综合题该如何理清思路?%>_
知识要点归纳:
就要考试了,如果你平时二次函数的题就做不下来的话,我建议你先不要研究它了.前两问会做就可以了.剩下的时间好好复习下前边儿的薄弱环节. 毕竟如果题难的话大家都不会做,白耗时间 ,也不一定要拿满分的.
2:2010北京中考数学二次函数压轴题在平面直角坐标系xOy中,抛物线y=-(m-1)/4x2+5m/4*x+m2-3m+2(注:x和m是未知数,未知数后面的2是平方,*是乘号)与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线
知识要点归纳:
1)因为二次函数过原点 所以 带入(0,0) m=1或2 因为是二次函数所以 m=2
所以y=-0.25xx+2.5x 所以 B:(2,4)
2)OB为y= 2x
故 OD为y=4x 不难求得OC为一= 1/3*x 又有C在抛物线上 x大于零的部分 所以Xc=34/3 Xp=68/9
时间快到了 没打完 不好意思……
3:【2010年底某市汽车拥有量为100万辆,而截止到2012年底,该市的汽车拥有量已达到144万辆.(1)求2010年底至2012年底该市汽车拥有量的年平均增长率;(2)该市交通部门为控制汽车拥有量的增】
知识要点归纳:
(1)设2010年底至2012年底该市汽车拥有量的年平均增长率是x,
根据题意,100(1+x)2=144
1+x=±1.2
∴x1=0.2=20% x2=-2.2(不合题意,舍去)
答:2010年底至2012年底该市汽车拥有量的年平均增长率是20%.
(2)设2012年底到2013年底该市汽车拥有量的年平均增长率为y,
根据题意得:144(1+y)-144×10%≤155.52
解得:y≤0.18
答:2012年底至2013年底该市汽车拥有量的年增长率要控制在不超过18%能达到要求.
4:如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.(1)求这个二次函数的解析式;(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求
知识要点归纳:
①∵函数的图象与x轴相交于O,
∴0=k+1,
∴k=-1,
∴y=x2-3x,
②假设存在点B,过点B做BD⊥x轴于点D,
∵△AOB的面积等于6,
∴1 2
当0=x2-3x,
x(x-3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2-3x,
解得:x=4或x=-1(舍去).
又∵顶点坐标为:( 1.5,-2.25).
∵2.25<4,
∴x轴下方不存在B点,
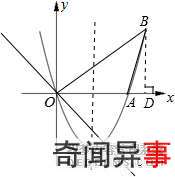
∴点B的坐标为:(4,4);
③∵点B的坐标为:(4,4),
∴∠BOD=45°,BO=
4 2+4 2 |
| 2 |
当∠POB=90°,
∴∠POD=45°,
设P点横坐标为:x,则纵坐标为:x2-3x,
即-x=x2-3x,
解得x=2 或x=0,
∴在抛物线上仅存在一点P (2,-2).
∴OP=
2 2+2 2 |
| 2 |
使∠POB=90°,
∴△POB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
猜你喜欢:
1:今年初三了,明年就的中考了,可我数学那啥三角形对...
提示:三角形对等?? 是全等三角形和相似三角形证明吧! 首先呢,你先有弄清三角形全等条件: SSS边边边 SAS边角边&HL直角三角形斜边及一直角边 ASA角边角&AAS角角边 其实,你做全等三角形证明时先找有什麽是相等的,无论是角啊,边啊 在复杂点的话会...
2:怎么解中考数学压轴题:一般是二次函数,三角形相似....
提示:平时多做, 多问老师。 如果你认为你不是尖子的话建议你多归纳一下各几何图形的第一辅助线和其他辅助线方法 一般有3小题你肯定会做,第4小题不一定会做,那么这时候一定要舔辅助线,在二次函数 的图像上尝试构造相似,动态问题也是这个,多利用...
3:如何解答中考圆与相似三角形的问题
提示:判定相似三角形的最常用方法就是角相等,而圆中有关角相等的方法有很多。 在同圆或等圆中,同弧所对的圆心角相等,圆周角相等。 这样就能结合到一起了,作答时注意多观察,从已知向求证推。从求证向已知推, 证明题无非就是让已知和求证达到统一...
4:中考数学证明题为什么不能用相似三角形做
提示:通过回忆与浏览教材,搜集与课题有关的所有知识。由于课题本身所容纳的知识点的不同,有些知识在学生头脑中很快就会再现,而有些知识可能被遗忘。让学生通过回忆再现,搜集与课题有关的知识,弄清楚每一知识点的意义,这是梳理知识的重要基矗我...
5:有关2016年中考数学试题中相似三角形的题?一道大...
提示:发不了链接自己百度 儿讯网 每日更新上千个资料。资料包含小学到高中所有科目的课件、试卷、教案等。 如果找不到你想要的资料还可以在服务中心发布需求,网站将通过其它渠道帮助你寻找


